/Szkoła średnia/Zadania testowe

Zadanie nr 9886769

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole figury ograniczonej fragmentem wykresu funkcji 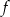f danej wzorem 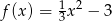f (x) = 13x 2 − 3 i osią 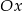Ox jest
A) mniejsze od 9 B) równe 18 C) większe od 9 D) większe od 18

Rozwiązanie

Ponieważ

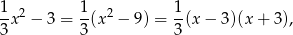
1 1 1 -x 2 − 3 = -(x 2 − 9) = -(x − 3)(x + 3 ), 3 3 3

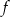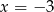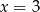wykresem funkcji f jest parabola o ramionach skierowanych w górę, miejscach zerowych x = − 3 i x = 3 , oraz wierzchołku w punkcie (0,− 3) .

PIC

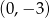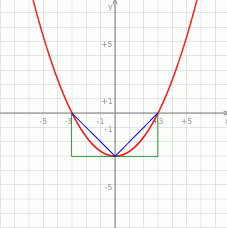
Oznaczmy przez 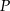P pole szukanego obszaru. Z rysunku widać, że trójkąt zaznaczony na rysunku ma pole mniejsze od szukanego pola. Policzmy pole tego trójkąta

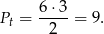
6-⋅3 Pt = 2 = 9 .

Policzmy jeszcze pole prostokąta o wierzchołkach w punktach 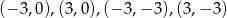(− 3,0),(3,0 ),(− 3,− 3),(3 ,−3 )

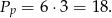
P = 6⋅ 3 = 18. p

Ponownie widać, że pole obszaru jest mniejsze niż obliczone pole prostokąta. Zatem otrzymujemy następujące nierówności

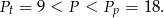
Pt = 9 < P < Pp = 1 8.

 
Odpowiedź: C

Wersja PDF