Zadanie nr 9944906
Jeśli wykres funkcji kwadratowej 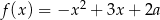 jest styczny do prostej
jest styczny do prostej 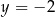 , to
, to
A) 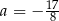 B)
B) 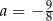 C)
C) 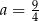 D)
D) 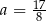
Rozwiązanie
Sposób I
Zapiszmy wzór funkcji 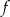 w postaci kanonicznej
w postaci kanonicznej
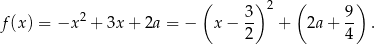
Wykresem tej funkcji jest więc parabola o ramionach skierowanych w dół i wierzchołku w punkcie 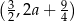 . Jeżeli wykres tej funkcji jest styczny do prostej
. Jeżeli wykres tej funkcji jest styczny do prostej 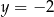 , to wierzchołek paraboli musi leżeć na tej prostej, tzn.
, to wierzchołek paraboli musi leżeć na tej prostej, tzn.
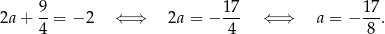
Sposób II
Wykres funkcji 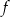 jest styczny do prostej
jest styczny do prostej 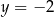 wtedy i tylko wtedy, gdy równanie
wtedy i tylko wtedy, gdy równanie
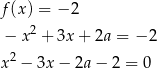
ma dokładnie jedno rozwiązanie. Aby tak było musi być spełniony warunek
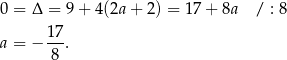
Sposób III
Wykresem funkcji 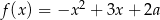 jest parabola o ramionach skierowanych w dół i pierwszej współrzędnej wierzchołka równej
jest parabola o ramionach skierowanych w dół i pierwszej współrzędnej wierzchołka równej
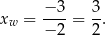
Jeżeli wykres tej funkcji ma jeden punkt wspólny z prostą 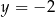 , to wierzchołek paraboli musi leżeć na tej prostej, tzn.
, to wierzchołek paraboli musi leżeć na tej prostej, tzn.
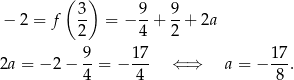
Odpowiedź: A

