/Szkoła średnia/Zadania testowe/Funkcje

Zadanie nr 1211120

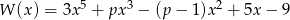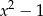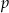Wielomian 5 3 2 W (x) = 3x + px − (p − 1)x + 5x − 9 jest podzielny przez dwumian x2 − 1 dla p równego
A) 6 B) 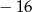− 16 C) 4 D)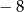 − 8

Wersja PDF

Rozwiązanie

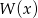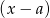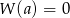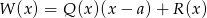Wielomian W (x) jest podzielny przez dwumian (x − a) wtedy i tylko wtedy, gdy W (a) = 0 (aby się o tym przekonać wystarczy podstawić x = a w równości W (x) = Q (x)(x − a) + R (x) ).

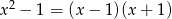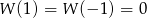Nas interesuje podzielność przez x2 − 1 = (x − 1 )(x+ 1) , więc sprawdzamy kiedy W (1) = W (− 1) = 0 .

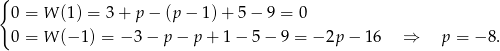
{ 0 = W (1) = 3 + p − (p − 1 )+ 5 − 9 = 0 0 = W (− 1) = − 3 − p − p + 1 − 5 − 9 = −2p − 16 ⇒ p = − 8.

 
Odpowiedź: D

Wersja PDF