Zadanie nr 9940745
Wartość wyrażenia 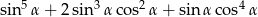 jest równa
jest równa
A) 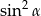 B)
B) 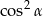 C)
C) 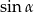 D)
D) 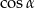
Rozwiązanie
Sposób I
Przekształćmy podane wyrażenie (wyciągamy 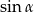 przed nawias).
przed nawias).
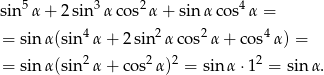
Sposób II
Łatwo sprawdzić, która odpowiedź jest poprawna licząc podane wyrażenie w jakimś konkretnym punkcie, np. dla 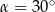 .
.
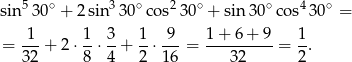
Tyle samo jest równy 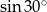 , więc poprawną odpowiedzią musi być
, więc poprawną odpowiedzią musi być 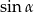 .
.
Odpowiedź: C

