/Szkoła średnia/Nierówności/Wymierne

Zadanie nr 6919501

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż algebraicznie i graficznie nierówność 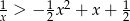1 1 2 1 x > − 2x + x+ 2 .

Rozwiązanie

Najpierw rozwiążmy algebraicznie.

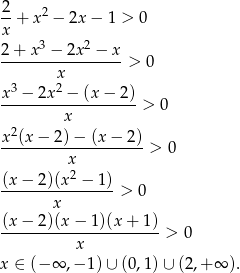
2 --+ x2 − 2x − 1 > 0 x 2+--x3 −-2x2-−-x- x > 0 x3 − 2x2 − (x − 2) -------------------> 0 x x2(x-−-2)-−-(x-−-2)- x > 0 2 (x−--2)(x--−-1)-> 0 x (x− 2)(x − 1)(x + 1) ----------x-----------> 0 x ∈ (− ∞ ,−1 )∪ (0,1) ∪ (2,+ ∞ ).

Teraz rozwiązujemy graficznie. Rysujemy wykresy obu stron.

PIC

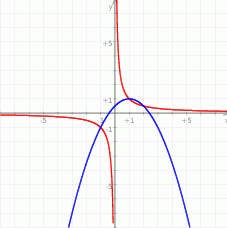
Parabola z prawej strony ma wierzchołek 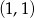(1,1) i ramiona skierowane w dół. Z obrazka powinno być widać, że wykresy przecinają się w 3 punktach. Można je odgadnąć z wykresu: 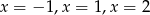x = − 1 ,x = 1,x = 2 i sprawdzić algebraicznie. Mamy zatem

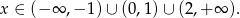
x ∈ (− ∞ ,−1 )∪ (0,1) ∪ (2,+ ∞ ).

 
Odpowiedź: x ∈ (− ∞ ,− 1) ∪ (0,1)∪ (2 ,+ ∞ )

Wersja PDF