/Szkoła średnia/Nierówności/Wymierne

Zadanie nr 7239585

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 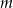m nierówność 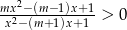mx2−-(m-−1)x+1 x2−(m+ 1)x+1 > 0 jest prawdziwa dla każdej liczby x ∈ R ?

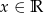Rozwiązanie

Zauważmy, że w mianowniku mamy funkcję kwadratową z dodatnim współczynnikiem przy 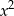x2 . Musimy najpierw sprawdzić kiedy ta funkcja nie ma miejsc zerowych (aby dziedziną danej funkcji był zbiór R ).

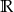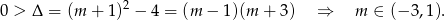
0 > Δ = (m + 1)2 − 4 = (m − 1)(m + 3) ⇒ m ∈ (− 3,1).

Zauważmy, że ten warunek gwarantuje nam, że mianownik jest dodatni, pozostaje nam więc nierówność

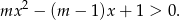
mx 2 − (m − 1)x + 1 > 0.

Aby była ona zawsze prawdziwa musi być 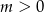m > 0 (trzeba też sprawdzić przypadek 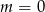m = 0 !) oraz Δ < 0 .

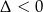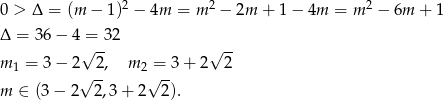
0 > Δ = (m − 1)2 − 4m = m 2 − 2m + 1− 4m = m 2 − 6m + 1 Δ = 3 6− 4 =√ -32 √ -- m1 = 3− 2 2, m 2 = 3 + 2 2 √ -- √ -- m ∈ (3 − 2 2 ,3+ 2 2).

Łącząc otrzymane warunki mamy

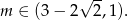
√ -- m ∈ (3− 2 2,1).

 
Odpowiedź: √ -- m ∈ (3− 2 2,1)

Wersja PDF