/Szkoła średnia/Zadania testowe/Równania

Zadanie nr 1383341

Dodaj do ulubionych
Dodaj do rozwiązanych

Równanie 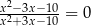x2−3x−-10- x2+3x− 10 = 0
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma dokładnie trzy rozwiązania

Rozwiązanie

Sprawdzamy kiedy zeruje się mianownik.

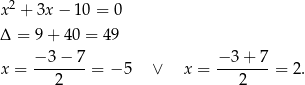
2 x + 3x − 10 = 0 Δ = 9+ 40 = 49 − 3− 7 − 3+ 7 x = -------= − 5 ∨ x = ------- = 2. 2 2

Teraz znajdziemy pierwiastki licznika

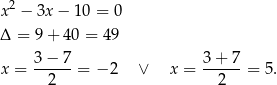
x2 − 3x − 10 = 0 Δ = 9+ 40 = 49 3− 7 3+ 7 x = -----= − 2 ∨ x = ------= 5. 2 2

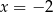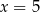Zatem licznik zeruje się dla x = −2 i x = 5 . Liczby te nie są miejscami zerowymi mianownika, więc równanie ma 2 pierwiastki.  
Odpowiedź: C

Wersja PDF