Zadanie nr 5040610
Funkcje kwadratowe 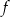 i
i 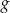 określone są wzorami
określone są wzorami 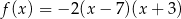 i
i 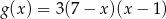 . Liczby
. Liczby 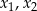 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 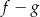 . Zatem
. Zatem
A) 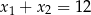 B)
B) 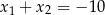 C)
C) 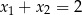 D)
D) 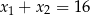
Rozwiązanie
Zauważmy, że
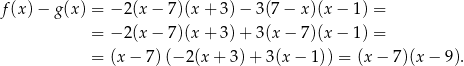
Miejscami zerowymi tej funkcji są więc liczby 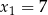 i
i 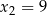 . Zatem
. Zatem
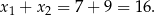
Odpowiedź: D

