/Szkoła średnia/Zadania testowe/Równania

Zadanie nr 5133011

Dodaj do ulubionych
Dodaj do rozwiązanych

Pierwiastkami trójmianu kwadratowego 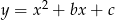2 y = x + bx + c są liczby -4 i 6. Wynika stąd, że
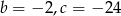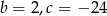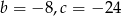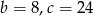
A) b = − 2,c = − 24 B) b = 2,c = − 2 4 C) b = − 8,c = − 2 4 D) b = 8,c = 24

Rozwiązanie

Sposób I

Jeżeli pierwiastkami trójmianu mają być liczby -4 i 6 to musi mieć on postać

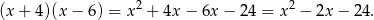
2 2 (x + 4)(x − 6 ) = x + 4x − 6x − 24 = x − 2x− 24.

Zatem 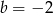b = − 2 i c = − 24 .

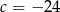Sposób II

Podstawiamy podane liczby i porównujemy do 0.

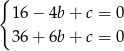
{ 16 − 4b + c = 0 36 + 6b + c = 0

Podstawiamy 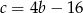c = 4b − 16 z pierwszego równania do drugiego i mamy

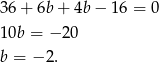
36 + 6b + 4b − 16 = 0 10b = − 20 b = − 2.

Zatem 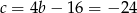c = 4b − 16 = − 24 .

Sposób III

Skorzystamy ze wzorów Viète’a

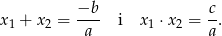
x + x = −b-- i x ⋅ x = c-. 1 2 a 1 2 a

Liczymy

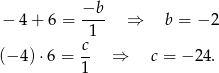
− 4+ 6 = −b-- ⇒ b = − 2 1 c- (− 4)⋅ 6 = 1 ⇒ c = − 24.

 
Odpowiedź: A

Wersja PDF