/Szkoła średnia/Zadania testowe/Równania

Zadanie nr 6963637

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczba różnych pierwiastków równania 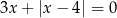3x + |x − 4| = 0 jest równa
A) 0 B) 1 C) 2 D) 3

Rozwiązanie

Sposób I

Lewą stronę równania możemy zapisać w postaci

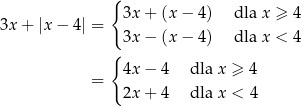
{ 3x + (x − 4) dla x ≥ 4 3x + |x − 4| = 3x − (x − 4) dla x < 4 { 4x − 4 dla x ≥ 4 = 2x + 4 dla x < 4

Łatwo teraz naszkicować wykres tej funkcji.

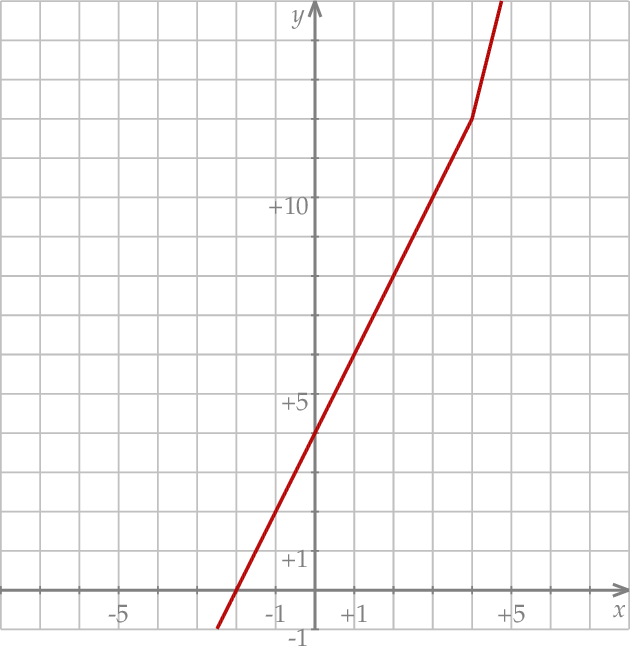
ZINFO-FIGURE

Z wykresu widać, że dane równanie ma dokładnie jedno rozwiązanie.

Sposób II

Jeżeli 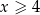x ≥ 4 , to mamy równanie

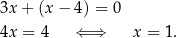
3x + (x − 4) = 0 4x = 4 ⇐ ⇒ x = 1 .

Liczba ta nie spełnia jednak warunku 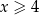x ≥ 4 .

Jeżeli natomiast 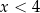x < 4 , to mamy równanie

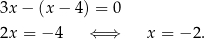
3x − (x − 4) = 0 2x = − 4 ⇐ ⇒ x = − 2 .

Równanie ma więc tylko jedno rozwiązanie.  
Odpowiedź: B

Wersja PDF