Zadanie nr 8112664
Dany jest układ równań: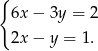 
Prawdziwe jest zdanie:
A) jednym z rozwiązań układu jest para liczb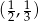 
B) układ równań ma nieskończenie wiele rozwiązań
C) układ równań nie ma rozwiązań
D) układ równań ma dokładnie jedno rozwiązanie
Rozwiązanie
Sposób I
Rozwiązujemy układ równań odejmując od pierwszego równania drugie pomnożone przez 3 (żeby skrócić 
).
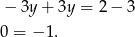
Jest to więc układ sprzeczny (nie ma rozwiązań).
Sposób II
Jeżeli pomnożymy drugie równanie układu stronami przez 3, to otrzymamy układ:
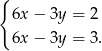
Widać gołym okiem, że jest to układ sprzeczny, bo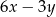 
nie może być jednocześnie równe 2 i 3.
Odpowiedź: C
