/Szkoła średnia/Zadania testowe/Funkcje - wykresy

Zadanie nr 1136774

Dodaj do ulubionych
Dodaj do rozwiązanych

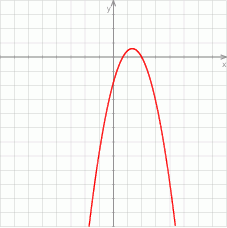
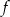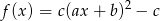Na rysunku przedstawiono fragment wykresu funkcji f określonej wzorem f (x) = c(ax + b)2 − c .

PIC

Współczynniki 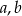a,b i c spełniają warunki:
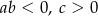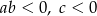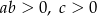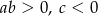
A) ab < 0 , c > 0 B) ab < 0, c < 0 C) ab > 0 , c > 0 D) ab > 0 , c < 0

Rozwiązanie

Przekształćmy dany wzór funkcji f .

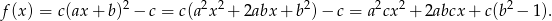
2 2 2 2 2 2 2 f(x) = c(ax + b ) − c = c(a x + 2abx + b )− c = a cx + 2abcx + c(b − 1 ).

Ramiona paraboli będącej wykresem funkcji 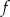f są skierowane w dół, więc na pewno 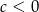c < 0 . Widać ponadto, że pierwsza współrzędna jej wierzchołka jest dodatnia, więc

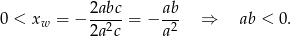
2abc ab 0 < xw = − ---2-= − -2- ⇒ ab < 0. 2a c a

 
Odpowiedź: B

Wersja PDF