Zadanie nr 1312413
Osią symetrii wykresu funkcji 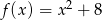 jest prosta o równaniu
jest prosta o równaniu
A) 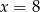 B)
B) 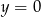 C)
C) 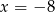 D)
D) 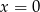
Rozwiązanie
Osią symetrii paraboli będącej wykresem funkcji kwadratowej jest pionowa prosta przechodząca przez jej wierzchołek.
Sposób I
Pierwszą współrzędną wierzchołka łatwo wyznaczyć:
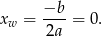
Zatem osią symetrii jest prosta 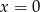 .
.
Sposób II
Parabola 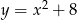 powstaje z paraboli
powstaje z paraboli 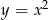 przez przesunięcie o 8 jednostek do góry, zatem jej oś symetrii jest taka sama jak oś symetrii paraboli
przez przesunięcie o 8 jednostek do góry, zatem jej oś symetrii jest taka sama jak oś symetrii paraboli 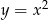 , czyli prosta
, czyli prosta 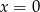 .
.
Odpowiedź: D

