Zadanie nr 4002318
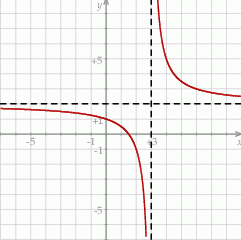
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 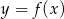 , której dziedziną jest zbiór
, której dziedziną jest zbiór 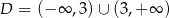 .
.
Równanie 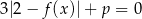 z niewiadomą
z niewiadomą  ma dokładnie dwa rozwiązania tylko wtedy, gdy
ma dokładnie dwa rozwiązania tylko wtedy, gdy
A) 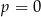 B)
B) 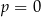 lub
lub 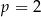 C)
C) 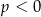 D)
D) 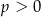
Rozwiązanie
Jeżeli 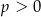 to równanie jest oczywiście sprzeczne (bo wtedy lewa strona równania jest dodatnia). Musi więc być
to równanie jest oczywiście sprzeczne (bo wtedy lewa strona równania jest dodatnia). Musi więc być 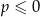 .
.
Sposób I
Spróbujmy rozwiązać dane równanie – korzystamy z tego, że 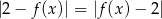 .
.
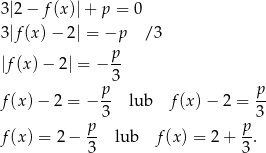
Widać teraz, że równanie ma zawsze dwa rozwiązania gdy 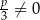 , czyli dla
, czyli dla 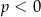 . Dla
. Dla 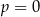 równanie jest sprzeczne.
równanie jest sprzeczne.
Sposób II
Szkicujemy wykres funkcji 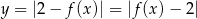 . W tym celu przesuwamy wykres
. W tym celu przesuwamy wykres 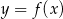 o 2 jednostki w dół i odbijamy część znajdującą się poniżej osi
o 2 jednostki w dół i odbijamy część znajdującą się poniżej osi 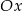 do góry.
do góry.
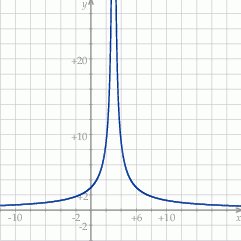
Z wykresu widać, że równanie 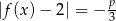 ma dwa rozwiązania wtedy i tylko wtedy, gdy
ma dwa rozwiązania wtedy i tylko wtedy, gdy 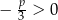 .
.
Odpowiedź: C

