Zadanie nr 8152018
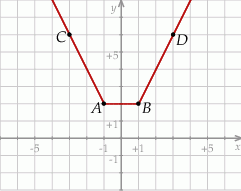
Na rysunku przedstawiono fragment wykresu funkcji 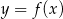 , który jest złożony z dwóch półprostych
, który jest złożony z dwóch półprostych 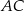 i
i 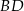 oraz odcinka
oraz odcinka 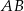 , gdzie
, gdzie 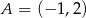 ,
, 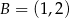 ,
, 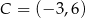 ,
, 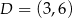 .
.
Wzór funkcji 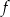 to
to
A) 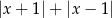 B)
B) 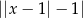 C)
C) 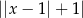 D)
D) 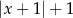
Rozwiązanie
Sposób I
Z podanego wykresu widać, że 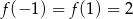 . Wśród podanych wzorów tylko wzór
. Wśród podanych wzorów tylko wzór
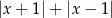
ma tę własność.
Sposób II
Widać, że funkcje dane wzorami
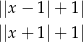
przyjmują wartość 1 (odpowiednio dla 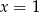 i
i 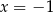 ). Podobnie, funkcja dana wzorem
). Podobnie, funkcja dana wzorem
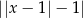
przyjmuje wartość 0 dla 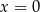 .
.
Z drugiej strony, najmniejsza wartość funkcji z danego wykresu to 2. Musi to być więc funkcja
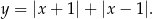
Odpowiedź: A

