Zadanie nr 1804074
Ile punktów wspólnych z osią 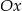 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 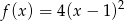 ?
?
A) 0 B) 1 C) 2 D) 3
Rozwiązanie
Sposób I
Funkcja 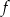 jest podana w postaci kanonicznej, więc możemy łatwo odczytać współrzędne wierzchołka:
jest podana w postaci kanonicznej, więc możemy łatwo odczytać współrzędne wierzchołka: 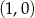 .
.
Ponieważ wierzchołek paraboli leży na osi 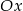 , więc parabola jest styczna do tej osi, czyli przecina ją w jednym punkcie.
, więc parabola jest styczna do tej osi, czyli przecina ją w jednym punkcie.
Sposób II
Przekształcamy wzór funkcji
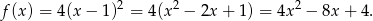
Sprawdzamy znak wyróżnika
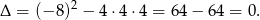
Zatem funkcja 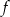 ma dokładnie jeden pierwiastek, więc jej wykres przecina oś
ma dokładnie jeden pierwiastek, więc jej wykres przecina oś 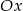 w jednym punkcie.
w jednym punkcie.
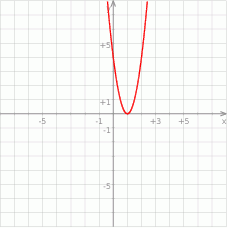
Dla ciekawskich wykres funkcji 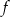 .
.
Odpowiedź: B

