Zadanie nr 5962785
Dana jest funkcja kwadratowa 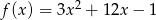 . Osią symetrii wykresu tej funkcji jest prosta
. Osią symetrii wykresu tej funkcji jest prosta
A) 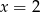 B)
B) 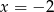 C)
C) 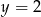 D)
D) 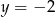
Rozwiązanie
Pamiętamy, że osią symetrii paraboli jest zawsze prosta pionowa przechodząca przez wierzchołek paraboli. Współrzędne wierzchołka paraboli danej wzorem 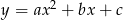 wyznaczamy ze wzoru
wyznaczamy ze wzoru 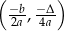 . Zauważmy, że z powyższego wzoru wystarczy wyznaczyć tylko pierwszą współrzędną. Liczymy
. Zauważmy, że z powyższego wzoru wystarczy wyznaczyć tylko pierwszą współrzędną. Liczymy
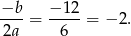
Na koniec obrazek
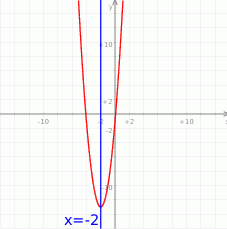
Odpowiedź: B

