/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola

Zadanie nr 6759194

Dodaj do ulubionych
Dodaj do rozwiązanych

Odległość wierzchołka paraboli 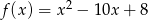2 f (x) = x − 10x + 8 od osi 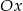Ox jest równa
A) 5 B) 17 C) 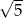√ -- 5 D) √ --- 17

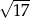
Rozwiązanie

Sposób I

Obliczamy wyznacznik

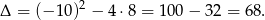
2 Δ = (−1 0) − 4 ⋅8 = 100− 32 = 68 .

Wyznaczamy współrzędne wierzchołka paraboli ze wzoru 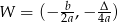b Δ W = (− 2a,− 4a)

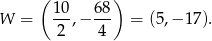
( ) W = 10,− 68- = (5,− 17). 2 4

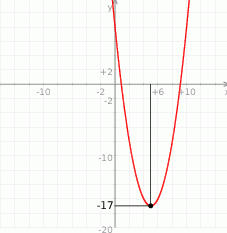
Odległość wierzchołka paraboli od osi 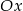Ox jest równa wartości bezwzględnej z drugiej współrzędnej wierzchołka, czyli jest równa 17.

PIC

Sposób II

Współrzędne wierzchołka mogliśmy również wyznaczyć sprowadzając podany wzór do postaci kanonicznej.

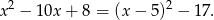
2 2 x − 10x + 8 = (x − 5) − 17.

Zatem wierzchołek ma współrzędne 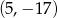(5,− 17) i jego odległość od osi 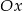Ox jest równa 17.  
Odpowiedź: B

Wersja PDF