Zadanie nr 9664391
Prosta o równaniu 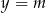 ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej
ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej 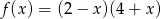 dla
dla
A) 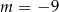 B)
B) 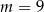 C)
C) 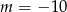 D)
D) 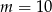
Rozwiązanie
Możemy zacząć od zrobienia szkicowego rysunku.
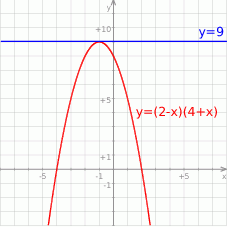
Sposób I
Wykresem podanej funkcji jest parabola o ramionach skierowanych w dół, a wykresem 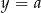 jest pozioma prosta. Powinno być teraz jasne, że te dwa wykresy będą miały dokładnie jeden punkt wspólny wtedy i tylko wtedy, gdy prosta ta przechodzi przez wierzchołek paraboli. Innymi słowy,
jest pozioma prosta. Powinno być teraz jasne, że te dwa wykresy będą miały dokładnie jeden punkt wspólny wtedy i tylko wtedy, gdy prosta ta przechodzi przez wierzchołek paraboli. Innymi słowy,  musi być równe drugiej współrzędnej wierzchołka podanej paraboli.
musi być równe drugiej współrzędnej wierzchołka podanej paraboli.
Pierwsza współrzędna to
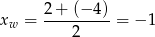
(jest dokładnie w środku między pierwiastkami), a więc druga współrzędna wierzchołka jest równa
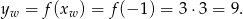
Zatem musi być 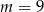 .
.
Sposób II
Zamiast szkicować obrazki, podstawmy 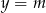 do wzoru paraboli i sprawdźmy, kiedy otrzymane równanie ma dokładnie jedno rozwiązanie.
do wzoru paraboli i sprawdźmy, kiedy otrzymane równanie ma dokładnie jedno rozwiązanie.
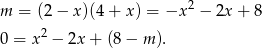
Teraz sprawdzamy kiedy 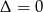 .
.
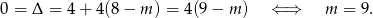
Odpowiedź: B

