Zadanie nr 5511172
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 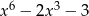 jest równe
jest równe
A) 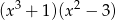 B)
B) 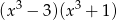 C)
C) 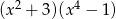 D)
D) 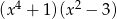
Rozwiązanie
Sposób I
Sprawdzamy podane odpowiedzi
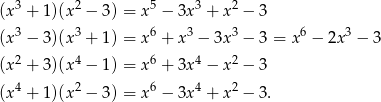
Sposób II
Zauważmy, że
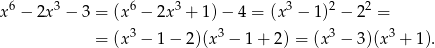
Sposób III
Zauważmy, że
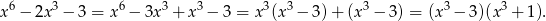
Sposób IV
Jeżeli podstawimy 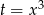 , to mamy trójmian kwadratowy
, to mamy trójmian kwadratowy 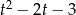 . Łatwo go rozłożyć licząc pierwiastki.
. Łatwo go rozłożyć licząc pierwiastki.
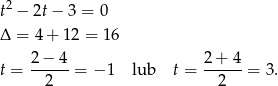
Zatem
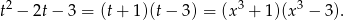
Odpowiedź: B

