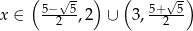Zadanie nr 1133731
Rozwiąż nierówność 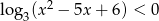 .
.
Rozwiązanie
Aby logarytm miał sens musimy mieć
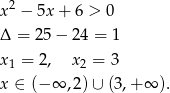
Przekształcamy teraz podaną nierówność
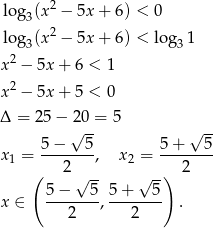
W połączeniu z warunkiem na dziedzinę daje to nam
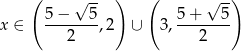
Odpowiedź: 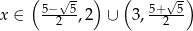
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 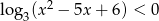 .
.
Aby logarytm miał sens musimy mieć
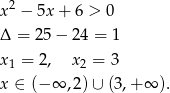
Przekształcamy teraz podaną nierówność
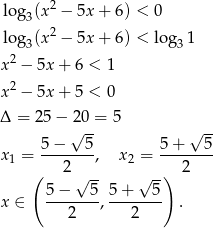
W połączeniu z warunkiem na dziedzinę daje to nam
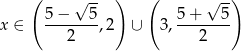
Odpowiedź: