/Szkoła średnia/Nierówności/Logarytmiczne

Zadanie nr 1152407

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 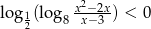x2−-2x lo g12(log8 x−3 ) < 0 .

Rozwiązanie

Ustalmy najpierw jaka jest dziedzina nierówności. Mianownik musi być niezerowy, czyli 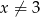x ⁄= 3 , oraz

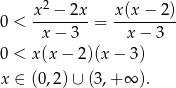
2 0 < x--−-2x- = x-(x−--2) x − 3 x − 3 0 < x(x − 2 )(x− 3) x ∈ (0,2) ∪ (3,+ ∞ ).

Powinniśmy jeszcze sprawdzić kiedy 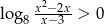2 lo g8 xx−−-2x3 > 0 , ale jak zaraz zobaczymy wyjdzie nam to ’za darmo’. Przekształcamy teraz nierówność

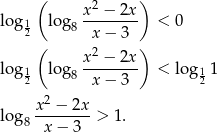
( ) x2 −-2x- log 12 lo g8 x− 3 < 0 ( 2 ) x-−--2x- log 12 lo g8 x− 3 < log 12 1 2 log x--−-2x-> 1. 8 x − 3

W tym miejscu widać, że rozwiązania powyższej nierówności automatycznie spełniają nierówność 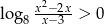lo g x2−-2x > 0 8 x− 3 .

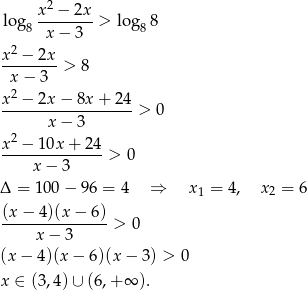
x2 − 2x log 8--------> log88 x − 3 x2 − 2x -x-−-3--> 8 2 x--−-2x-−-8x-+--24 > 0 x − 3 x2 − 10x + 24 -------------- > 0 x − 3 Δ = 100 − 96 = 4 ⇒ x1 = 4, x 2 = 6 (x-−-4)(x-−-6-)> 0 x− 3 (x − 4)(x − 6)(x − 3) > 0 x ∈ (3,4) ∪ (6,+ ∞ ).

 
Odpowiedź: x ∈ (3 ,4)∪ (6,+ ∞ )

Wersja PDF