Definicje Najważniejsze w całej zabawie z logarytmami to zrozumieć, co to jest logarytm.
Wyrażenie 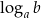 jest równe odpowiedzi na pytanie:
jest równe odpowiedzi na pytanie:
do jakiej potęgi należy podnieść  , żeby otrzymać
, żeby otrzymać 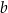 ?
?
To zdanie należy traktować jako definicję logarytmów i koniecznie trzeba je zapamiętać – jest to klucz do wszystkich ich własności. Przy pomocy wzorków zapisuje się to w postaci
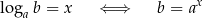
Od ręki możemy policzyć kilka prostych przykładów – w każdym z nich spróbujcie samodzielnie zgadnąć odpowiedź – i nie potrzebujemy do tego żadnych wzorów!
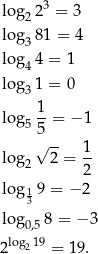
Jeżeli ktoś nie rozumie powyższych równości to ma małe szanse na sprawne posługiwanie się logarytmami, dlatego radzę się poprzyglądać do skutku.
Jeżeli rozumiemy już te wzorki, to powinny być jasne odrobinę ogólniejsze równości:
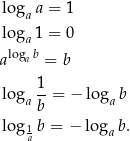
Tego typu wzory bywają bardzo użyteczne, ale jeżeli pamiętamy (i rozumiemy) definicję logarytmu, to nie trzeba ich się uczyć na pamięć, są one wtedy dość oczywiste.
Dla przykładu popatrzmy na trzeci wzorek: 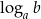 to jest taka liczba, że jak podniesiemy do niej
to jest taka liczba, że jak podniesiemy do niej  to wyjdzie
to wyjdzie 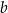 . I co robimy? – podnosimy do niej
. I co robimy? – podnosimy do niej  , więc wychodzi
, więc wychodzi 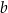 .
.
Dla treningu przeczytajmy jeszcze czwarty wzorek. Wiemy, że jak podniesiemy  do potęgi
do potęgi 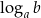 to wyjdzie
to wyjdzie 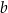 . Jeżeli więc podniesiemy
. Jeżeli więc podniesiemy  do potęgi
do potęgi 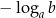 to wyjdzie
to wyjdzie 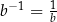 .
.
Obliczmy 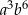 jeżeli
jeżeli 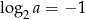 i
i 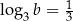 .
.
Z definicji logarytmu wiemy, że 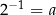 i
i 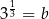 . Zatem
. Zatem
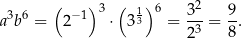
Wzorki W przypadku bardziej skomplikowanych wyrażeń, np. 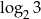 nie jesteśmy w stanie obliczyć tej liczby dokładnie – jest to po prostu potęga do jakiej trzeba podnieść 2, żeby wyszło 3. Jest to pewna liczba niewymierna, mniej więcej równa 1,58496... (powinno być jasne, że musi być między 1 a 2, bo
nie jesteśmy w stanie obliczyć tej liczby dokładnie – jest to po prostu potęga do jakiej trzeba podnieść 2, żeby wyszło 3. Jest to pewna liczba niewymierna, mniej więcej równa 1,58496... (powinno być jasne, że musi być między 1 a 2, bo 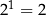 i
i 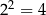 ). Symbol
). Symbol 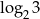 należy traktować jako oznacznie tej liczby. Pomimo, że nie znamy jej dokładnej wartości, możemy jednak o niej coś powiedzieć, np. bezpośrednio z definicji wiemy, że
należy traktować jako oznacznie tej liczby. Pomimo, że nie znamy jej dokładnej wartości, możemy jednak o niej coś powiedzieć, np. bezpośrednio z definicji wiemy, że 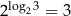 . Są też ciekawsze własności.
. Są też ciekawsze własności.
Sprawdźmy że 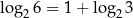 .
.
Myślimy o tym następująco: do jakiej potęgi trzeba podnieść 2, żeby wyszło 6? Ponieważ 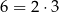 , musimy podnieść 2 do potęgi 1 (dwójka w rozkładzie) i jeszcze do
, musimy podnieść 2 do potęgi 1 (dwójka w rozkładzie) i jeszcze do 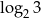 (trójka w rozkładzie).
(trójka w rozkładzie).
Sytuacja jest podobna jak z pierwiastkami: mało kto potrafi podać nawet przybliżoną wartość 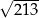 , ale jest jasne, że
, ale jest jasne, że 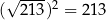 czy
czy 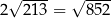 .
.
Pomimo, że takie kombinowanie nie jest bardzo trudne, można to zrobić szybciej korzystając z następujących wzorów:
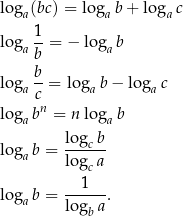
Nie będziemy tych wzorków uzasadniać, zamiast tego krótko je omówimy. Pierwszy wzór, który jest natychmiastową konsekwencją wzoru 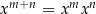 , jest zdecydowanie najważniejszą własnością logarytmów. Można go czytać tak: suma logarytmów to logarytm iloczynu. Wzór ten pojawia się w większości zadań z logarytmami – zapamiętać należy, że logarytmy dobrze zachowują się przy dodawaniu.
, jest zdecydowanie najważniejszą własnością logarytmów. Można go czytać tak: suma logarytmów to logarytm iloczynu. Wzór ten pojawia się w większości zadań z logarytmami – zapamiętać należy, że logarytmy dobrze zachowują się przy dodawaniu.
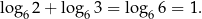
Drugi wzór to prosta konsekwencja definicji (można też go traktować jako przypadek szczególny 4 wzoru).
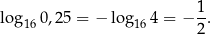
Trzeci wynika natychmiast z pierwszych dwóch i z grubsza mówi, że logarytmy dobrze się zachowują przy odejmowaniu.
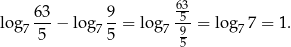
Czwarty wzór, wynikający z równości 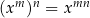 , bywa bardzo użyteczny w rachunkach, bo pozwala wyciągać potęgi przed logarytm.
, bywa bardzo użyteczny w rachunkach, bo pozwala wyciągać potęgi przed logarytm.
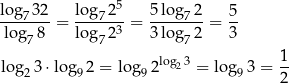
Przedostatni wzór to tzw. wzór na zmianę podstawy logarytmu. Jak nazwa wskazuje pozwala dowolnie zmieniać podstawę logarytmu.
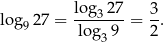
Jeszcze jeden przykład na ostatni wzór.
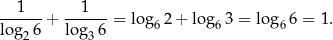
Logarytm dziesiętny i naturalny Jak zrobić tablice logarytmów? – w zasadzie się nie da, bo 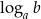 ma dwa argumenty i takie tablice byłyby ogromne. Z drugiej strony, mamy wzór na zmianę podstawy logarytmu i wystarczy znać logarytmy przy jednej ustalonej podstawie. Dlatego wyróżnia się dwie podstawy: 10 i
ma dwa argumenty i takie tablice byłyby ogromne. Z drugiej strony, mamy wzór na zmianę podstawy logarytmu i wystarczy znać logarytmy przy jednej ustalonej podstawie. Dlatego wyróżnia się dwie podstawy: 10 i 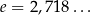 . Logarytm przy podstawie 10 nazywa się dzięsiętnym i oznacza
. Logarytm przy podstawie 10 nazywa się dzięsiętnym i oznacza 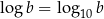 , a przy podstawie
, a przy podstawie  naturalnym i oznacza
naturalnym i oznacza 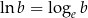 .
.
O ile nie trzeba specjalnie tłumaczyć dlaczego logarytm przy podstawie 10 jest wyróżniony, to aby dobrze zrozumieć fenomen logarytmu naturalnego trzeba umieć liczyć pochodne funkcji wykładniczych – ponieważ takie pochodne zniknęły ze szkoły, logarytm naturalny też jest w niej marginalizowany. Warto jednak wiedzieć, że taki jest.
Tips & Tricks
1Pamiętajmy, że wzory na sumę i różnicę logarytmów wymagają, aby logarytmy miały tę samą podstawę. Jeżeli nie mają, to możemy spróbować ją zmienić ze wzoru na zamianę podstawy logarytmu.
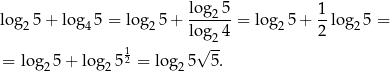
2Czasem może spotkać się z potrzebą uproszczenia wyrażenia, w którym mamy iloczyny logarytmów, np.
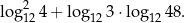
Ponieważ nie ma wzoru na iloczyn logarytmów w takiej sytuacji staramy się wyłączyć wspólny czynnik przed nawias i skorzystać ze wzoru na sumę logarytmów.
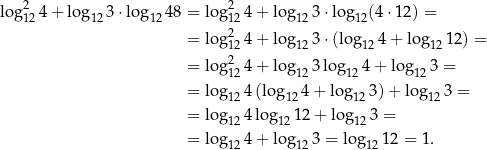
3Wprawdzie wzór na logarytm iloczynu zwykle podaje się tylko dla dwóch liczb, ale jest on prawdziwy dla dowolnej liczby czynników.
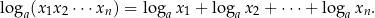
Obliczmy sumę
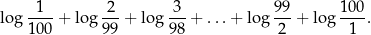
Ze wzoru na logarytm iloczynu, suma ta jest równa:
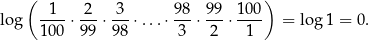
4Duża liczba wzorków z logarytmami sprawia, że mamy podobną sytuację jak z funkcjami trygonometrycznymi: ta sama liczba może być zapisana na wiele różnych sposobów.
W poprzednim podpunkcie sprawdziliśmy, że
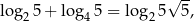
ale mogliśmy też liczyć tak
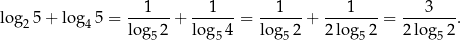
5Większość szkolnych kalkulatorów/tablic pozwala znaleźć tylko wartości logarytmów dziesiętnych. Jak w takim razie wyliczyć inny logarytm? – korzystamy ze wzoru na zamianę podstawy logarytmu
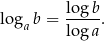
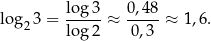
Tu zaczynamy dotykać delikatnego problemu szacowania błędu obliczeń: jeżeli dzielimy dwie liczby, które znamy z dokładnością do 0,01 to trudno jest przewidzieć z jaką dokładnością znamy wynik (zależy to od wartości liczby, przez którą dzielimy). Aby to zrozumieć, wystarczy wziąć przybliżenie 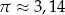 i podzielić przez 10. Wtedy wynik znamy z dokładnością do 0,001. Ale jak podzielimy przez
i podzielić przez 10. Wtedy wynik znamy z dokładnością do 0,001. Ale jak podzielimy przez 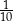 (czyli pomnożymy przez 10), to wynik znamy tylko z dokładnością do 0,1. W naszym przykładzie dzieliliśmy przez 0,3, więc wyniku na pewno nie znamy z dokładnością do dwóch miejsc po przecinku.
(czyli pomnożymy przez 10), to wynik znamy tylko z dokładnością do 0,1. W naszym przykładzie dzieliliśmy przez 0,3, więc wyniku na pewno nie znamy z dokładnością do dwóch miejsc po przecinku.
6Jest sporo zadań typu ’uprość wyrażenie’, w których występują logarytmy o różnych podstawach – zwykle pierwszą rzeczą do zrobienia jest sprowadzenie wszystkich logarytmów do wspólnej podstawy – im mniejszej tym lepiej. Np. jeżeli w zadaniu są logarytmy o podstawie 2,3,6,9 to za wspólną podstawę najlepiej wziąć 2 lub 3. Jeżeli nie widać jaką wziąć wspólną podstawę, to zawsze możemy pozamieniać wszystko na logarytmy dziesiętne lub naturalne.
Obliczmy wartość wyrażenia 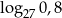 jeżeli
jeżeli 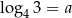 i
i 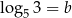 .
.
Liczba która się wyróżnia w podanej treści to 3 (jest w każdym składniku, bo 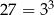 ), więc zamieniamy podstawę wszystkich logarytmów na 3.
), więc zamieniamy podstawę wszystkich logarytmów na 3.
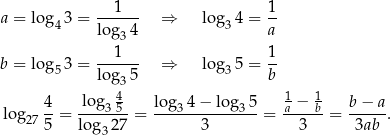
Sprawdźmy, kiedy liczby 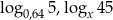 i
i 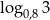 są kolejnymi wyrazami ciągu arytmetycznego.
są kolejnymi wyrazami ciągu arytmetycznego.
Interesujący nas warunek będzie spełniony jeżeli środkowa liczba będzie średnią arytmetyczną pozostałych dwóch. Liczmy (zamieniamy wszystkie logarytmy na dziesiętne).
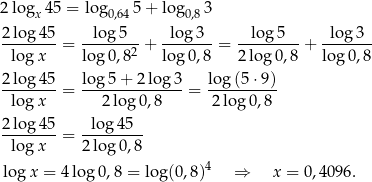
7Jedno z popularnych zastosowań logarytmów, to ’zdejmowanie na dół wykładników’, czyli logarytmowanie stronami.
Rozwiążmy równanie 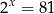 .
.
Logarytmujemy równanie stronami logarytmem przy podstawie 2.
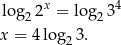
Uzasadnijmy, że liczby 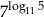 i
i 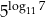 są równe.
są równe.
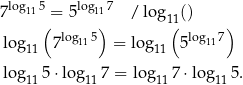
Otrzymana równość jest oczywiście prawdziwa.
Ile cyfr ma liczba 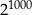 ?
?
Pytanie można przeformułować tak: dla jakiej liczby całkowitej 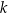 , mamy nierówność
, mamy nierówność
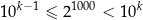
(np. liczby trzycyfrowe to te, które są nie mniejsze od 100 i mniejsze od 1000). Jeżeli zlogarytmujemy tę równość stronami (logarytmem dziesiętnym) to mamy
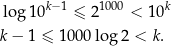
Pytanie zatem brzmi jak jest część całkowita liczby 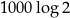 . Ponieważ mnożymy przez 1000 potrzebujemy do tego wartość
. Ponieważ mnożymy przez 1000 potrzebujemy do tego wartość 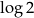 z dokładnością do 0,001. Oczywiście to żaden problem dla kalkulatora i mamy
z dokładnością do 0,001. Oczywiście to żaden problem dla kalkulatora i mamy
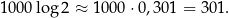
Zatem liczba 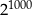 ma 302 cyfry (bo w nierówności ma być
ma 302 cyfry (bo w nierówności ma być 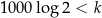 ).
).
8Żeby nie zaciemniać obrazka nie przejmowaliśmy się na razie dziedziną logarytmu, ale warto pamiętać, że w wyrażeniu 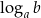 musi być
musi być 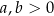 i
i 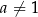 . Takie rzeczy zaczynają być bardzo ważne, gdy mamy parametry i nie wiemy dokładnie jaki mają znak.
. Takie rzeczy zaczynają być bardzo ważne, gdy mamy parametry i nie wiemy dokładnie jaki mają znak.
Rozwiążmy równanie 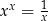 , gdzie
, gdzie 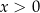 . Logarytmujemy stronami logarytmem przy podstawie
. Logarytmujemy stronami logarytmem przy podstawie  .
.
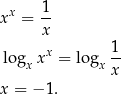
Mieliśmy szukać tylko dodatnich rozwiązań, więc równanie jest sprzeczne.
Na pewno? Logarytmować przy podstawie  mogliśmy tylko dla
mogliśmy tylko dla 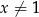 , więc
, więc 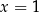 musimy sprawdzić osobno. I tak się składa, że to akurat jest rozwiązanie.
musimy sprawdzić osobno. I tak się składa, że to akurat jest rozwiązanie.
Spróbujmy rozwiązać równanie ![lo g[x(x+ 3)]− log [x (x+ 2)] = lo g2](https://img.zadania.info/por/0020995/HporT92x.png) .
.
Liczymy
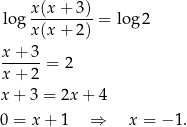
Rachunek wygląda niewinnie, ale 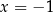 wcale nie jest rozwiązaniem równania! (Bo argumenty logarytmów wychodzą ujemne.) Z drugiej strony,
wcale nie jest rozwiązaniem równania! (Bo argumenty logarytmów wychodzą ujemne.) Z drugiej strony, 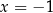 jest rozwiązaniem równania
jest rozwiązaniem równania 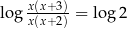 . Po prostu lewa i prawa strona równości
. Po prostu lewa i prawa strona równości
![lo g[x(x + 3)]− log [x (x+ 2)] = lo g x(x-+-3)- x(x + 2)](https://img.zadania.info/por/0020995/HporT97x.png)
mają różne dziedziny.
9Widzieliśmy przed chwilą, że trzeba bardzo ostrożnie używać wzorów z logarytmami, gdyż na ogół zmieniają one dziedzinę przekształcanego wyrażenia. W niektórych sytuacjach wygodne jest połączenie wzorów z logarytmami razem z wartością bezwzględną, co znacznie zwiększa możliwości ich zastosowania.
Dziedzina prawej strony wzoru 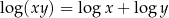 jest znacznie mniejsza od dziedziny lewej strony. Jeżeli jednak zapiszemy ten wzór w postaci
jest znacznie mniejsza od dziedziny lewej strony. Jeżeli jednak zapiszemy ten wzór w postaci
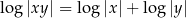
to dziedziny obu stron są dokładnie takie same.
Podobnie jest z wzorem 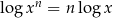 . Jeżeli
. Jeżeli 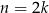 jest liczba całkowitą parzystą, to lewa strona ma sens dla dowolnych niezerowych liczb
jest liczba całkowitą parzystą, to lewa strona ma sens dla dowolnych niezerowych liczb  , a prawa tylko dla liczb dodatnich. Jeżeli jednak napiszemy ten wzór w postaci
, a prawa tylko dla liczb dodatnich. Jeżeli jednak napiszemy ten wzór w postaci
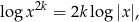
to dziedziny obu stron są identyczne. O wzorze tym należy myśleć jak o odpowiedniku wzoru
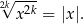
Rozwiążmy równanie 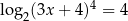 .
.
Mamy
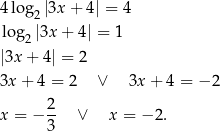
10 Często wykorzystywany motyw w zadaniach szkolnych to fakt, że logarytm zamienia ciąg geometryczny na arytmetyczny.
Jeżeli ciąg 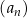 jest geometryczny, to iloraz
jest geometryczny, to iloraz 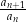 nie zależy od
nie zależy od  . Jeżeli tę równość zlogarytmujemy
. Jeżeli tę równość zlogarytmujemy
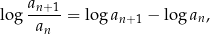
to widzimy, że różnica ta nie zależy od  , czyli ciąg
, czyli ciąg 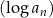 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
11Niezwykła użyteczność logarytmu wynika z faktu, że zamienia on mnożenie na dodawanie. Jeżeli popatrzymy na wzór 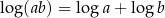 to widać, że jeżeli umiemy zamieniać liczby na logarytmy i odwrotnie (np. mamy tablice logarytmów), to zamiast mnożyć liczby
to widać, że jeżeli umiemy zamieniać liczby na logarytmy i odwrotnie (np. mamy tablice logarytmów), to zamiast mnożyć liczby  i
i 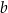 możemy dodać ich logarytmy. I co z tego? Żeby to zrozumieć trzeba się przenieść w czasy przedkalkulatorowe: proponuję spróbować pisemnie wymnożyć 10 liczb 3 cyfrowych, a wtedy będzie jasne dlaczego dodawanie jest o wiele prostsze od mnożenia. Nawet w czasach współczesnych procesorów, mnożenie jest bardzo czasochłonną operacją i zamiana go na dodawanie dramatycznie przyśpiesza obliczenia.
możemy dodać ich logarytmy. I co z tego? Żeby to zrozumieć trzeba się przenieść w czasy przedkalkulatorowe: proponuję spróbować pisemnie wymnożyć 10 liczb 3 cyfrowych, a wtedy będzie jasne dlaczego dodawanie jest o wiele prostsze od mnożenia. Nawet w czasach współczesnych procesorów, mnożenie jest bardzo czasochłonną operacją i zamiana go na dodawanie dramatycznie przyśpiesza obliczenia.
Policzmy 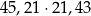 .
.
Sprawdzamy w tablicach (na kalkulatorze :)), że
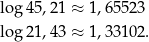
Dodajmy te liczby i mamy 2,98625. Teraz szukamy jakiej liczby to jest logarytm (czyli liczymy 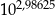 ). Wychodzi 968,84. Osobny problem to szacowanie jaki popełniamy błąd, ale nie będziemy się tym zajmować.
). Wychodzi 968,84. Osobny problem to szacowanie jaki popełniamy błąd, ale nie będziemy się tym zajmować.
Tego typu rachunki miały fundamentalne znacznie w czasach rewolucji przemysłowej, a suwak logarytmiczny jeszcze nie tak dawno temu był nieodłącznym atrybutem każdego inżyniera.
12Przed chwilą przekonywałem, że logarytmy pozwalają łatwo mnożyć liczby, ale to nie wszystko. Dzięki wzorowi
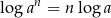
pozwalają też szybko liczyć wartości funkcji wykładniczych oraz pierwiastków.
Policzmy 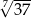 .
.
Zamiast liczyć interesującą nas liczbę, liczymy jej logarytm.
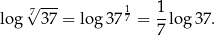
Teraz odszukujemy wartość 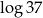 w tablicach (na suwaku), dzielimy przez 7
w tablicach (na suwaku), dzielimy przez 7
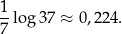
Na koniec szukamy liczby, której jest to logarytm. Wyjdzie
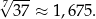
Oczywiście takie rachunki są dość archaiczne w dzisiejszych czasach i pozostają ciekawostką historyczną.

