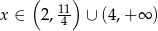Zadanie nr 6404962
Rozwiąż nierówność 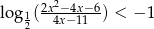 .
.
Rozwiązanie
Sprawdźmy najpierw kiedy wyrażenie pod logarytmem jest dodatnie
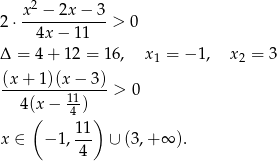
Teraz przekształćmy podaną nierówność
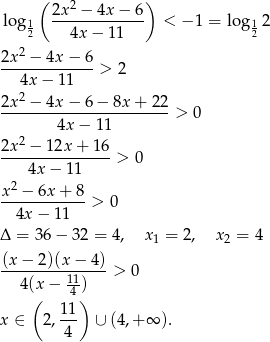
Odpowiedź: 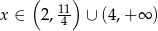
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 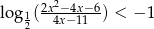 .
.
Sprawdźmy najpierw kiedy wyrażenie pod logarytmem jest dodatnie
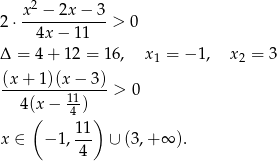
Teraz przekształćmy podaną nierówność
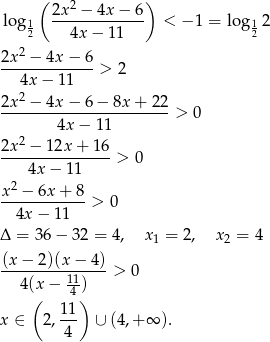
Odpowiedź: