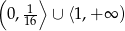Zadanie nr 6987927
Rozwiąż nierówność 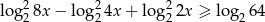 .
.
Rozwiązanie
Dziedziną podanej nierówności jest przedział 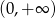 . Przekształćmy nierówność
. Przekształćmy nierówność
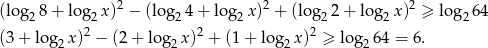
Żeby sobie trochę uprościć zapis, oznaczmy 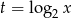 .
.
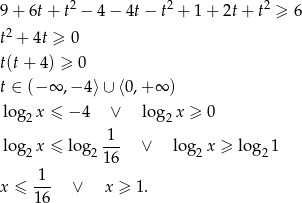
Uwzględniając dziedzinę mamy
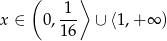
Odpowiedź: 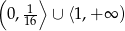
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 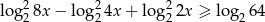 .
.
Dziedziną podanej nierówności jest przedział 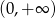 . Przekształćmy nierówność
. Przekształćmy nierówność
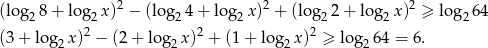
Żeby sobie trochę uprościć zapis, oznaczmy 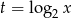 .
.
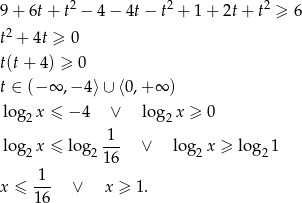
Uwzględniając dziedzinę mamy
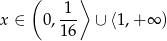
Odpowiedź: