/Szkoła średnia/Nierówności/Logarytmiczne

Zadanie nr 9555439

Dodaj do ulubionych
Dodaj do rozwiązanych

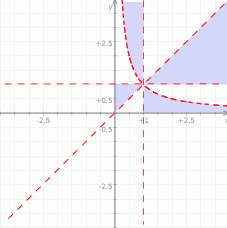
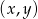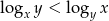Zaznacz w układzie współrzędnych zbiór punktów (x,y) , dla których współrzędne spełniają nierówność logx y < logy x .

Rozwiązanie

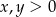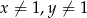Aby nierówność miała sens musi być x,y > 0 i x ⁄= 1,y ⁄= 1 . Przekształcamy podaną nierówność

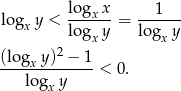
lo g y < logx-x = ---1-- x logx y logx y (lo g y)2 − 1 ----x--------< 0. logx y

Jeżeli podstawimy 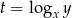t = logx y to mamy

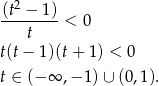
2 (t-−--1) t < 0 t(t− 1 )(t+ 1) < 0 t ∈ (− ∞ ,−1 )∪ (0,1).

Mamy zatem nierówności

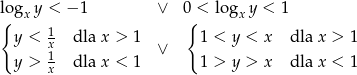
logx y < − 1 ∨ 0 < lo gxy < 1 { 1 { y < x dla x > 1 ∨ 1 < y < x dla x > 1 y > 1x dla x < 1 1 > y > x dla x < 1

Teraz bez trudu zaznaczamy ten obszar.

PIC

Wersja PDF