/Szkoła średnia/Nierówności/Logarytmiczne

Zadanie nr 9714015

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 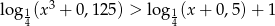3 lo g14(x + 0,125 ) > lo g14(x + 0,5) + 1 .

Rozwiązanie

Sprawdźmy najpierw jaka jest dziedzina nierówności.

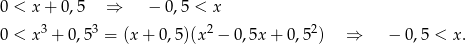
0 < x + 0,5 ⇒ − 0,5 < x 0 < x 3 + 0 ,53 = (x + 0,5)(x2 − 0,5x + 0 ,5 2) ⇒ − 0,5 < x.

W drugiej linijce skorzystaliśmy z tego, że trójmian w nawiasie nie ma pierwiastków (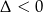Δ < 0 ). Przekształcamy podaną nierówność (korzystamy ze wzoru na sumę logarytmów).

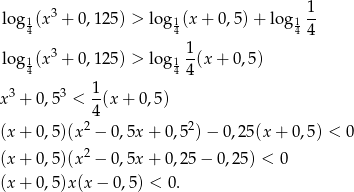
log (x 3 + 0,125) > log (x+ 0,5)+ lo g 1- 14 14 14 4 3 1 log 14(x + 0,125) > log 14--(x+ 0,5) 4 x3 + 0,53 < 1-(x+ 0,5) 4 (x+ 0,5)(x2 − 0,5x + 0,5 2) − 0,25 (x+ 0,5) < 0 2 (x+ 0,5)(x − 0,5x + 0,2 5− 0 ,25) < 0 (x+ 0,5)x(x − 0,5 ) < 0.

Ponieważ założyliśmy, że pierwszy nawias jest dodatni, pozostaje nam nierówność

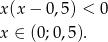
x(x− 0,5) < 0 x ∈ (0;0,5).

 
Odpowiedź: x ∈ (0;0 ,5 )

Wersja PDF