Zadanie nr 3417460
Zbiór 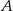 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 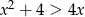 . Zatem
. Zatem
A) 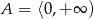 B)
B) 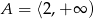 C)
C) 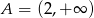 D)
D) 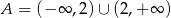
Rozwiązanie
Sposób I
Liczymy
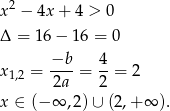
Sposób II
Mogliśmy też od razu zauważyć, że mamy do czynienia z pełnym kwadratem.
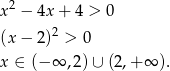
Odpowiedź: D
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Zbiór 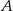 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 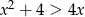 . Zatem
. Zatem
A) 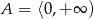 B)
B) 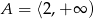 C)
C) 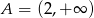 D)
D) 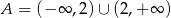
Sposób I
Liczymy
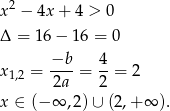
Sposób II
Mogliśmy też od razu zauważyć, że mamy do czynienia z pełnym kwadratem.
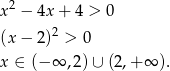
Odpowiedź: D
