/Szkoła średnia/Zadania testowe/Nierówności/Kwadratowe

Zadanie nr 7139439

Dodaj do ulubionych
Dodaj do rozwiązanych

Przedział 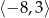⟨− 8,3⟩ jest zbiorem rozwiązań nierówności
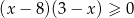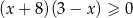
A) (x − 8)(3 − x) ≥ 0 B) (x+ 8)(3− x) ≥ 0
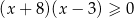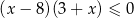
C) (x + 8)(x − 3) ≥ 0 D) (x − 8)(3 + x) ≤ 0

Rozwiązanie

Oczywiście wykresem każdej z powyższych funkcji jest parabola. Patrząc na podany przedział widać, że musi ona mieć miejsca zerowe 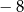− 8 i 3. To eliminuje odpowiedzi

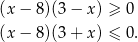
(x − 8 )(3− x ) ≥ 0 (x − 8 )(3+ x ) ≤ 0.

Rozwiązaniem nierówności

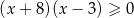
(x+ 8)(x − 3) ≥ 0

jest zbiór 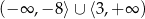(− ∞ ,− 8⟩ ∪ ⟨3,+ ∞ ) , więc zostaje

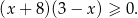
(x + 8 )(3− x ) ≥ 0.

Rzeczywiście, nierówność tę możemy zapisać w postaci

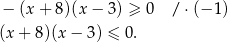
− (x + 8)(x − 3) ≥ 0 / ⋅(− 1) (x + 8)(x − 3) ≤ 0.

 
Odpowiedź: B

Wersja PDF