Zadanie nr 7941818
Rozwiązaniem nierówności 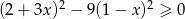 jest zbiór
jest zbiór
A) 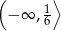 B)
B) 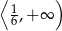 C)
C) 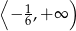 D)
D) 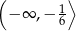
Rozwiązanie
Sposób I
Przekształcamy daną nierówność korzystając ze wzoru na różnicę kwadratów.
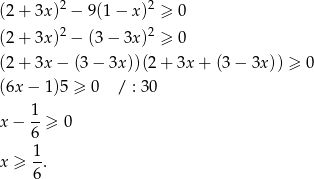
Sposób II
Przekształcamy daną nierówność korzystając ze wzorów na kwadrat sumy i różnicy.
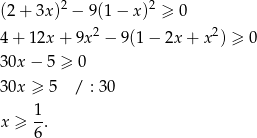
Odpowiedź: B

