Zadanie nr 1405738
Punkty 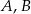 i
i 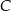 leżą na okręgu o środku
leżą na okręgu o środku 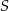 (zobacz rysunek).
(zobacz rysunek).
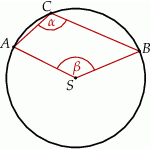
Miary  i
i 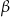 zaznaczonych kątów
zaznaczonych kątów 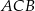 i
i 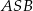 spełniają warunek
spełniają warunek 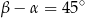 . Wynika stąd, że
. Wynika stąd, że
A) 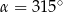 B)
B) 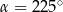 C)
C) 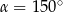 D)
D) 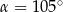
Rozwiązanie
Sposób I
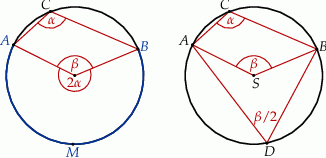
Korzystamy z faktu, że kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku (na danym obrazku jest to łuk 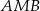 ).
).
Zatem
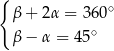
Odejmujemy od pierwszego równania drugie i mamy
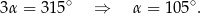
Sposób II
Jeżeli nie chcemy posługiwać się kątami wklęsłymi to dorysujmy punkt 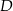 na na okręgu. Wtedy
na na okręgu. Wtedy
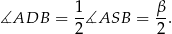
Zatem
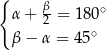
Dodajemy równania stronami i mamy
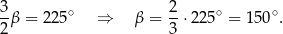
Stąd 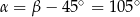 .
.
Odpowiedź: D

