Zadanie nr 1458403
Liczba przekątnych wszystkich ścian bocznych i podstawy pewnego graniastosłupa jest równa 182. Zatem podstawą tego graniastosłupa jest:
A) trzynastokąt B) czternastokąt C) piętnastokąt D) szesnastokąt
Rozwiązanie
Oznaczmy przez  liczbę wierzchołków podstawy graniastosłupa.
liczbę wierzchołków podstawy graniastosłupa.
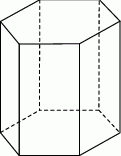
Każda ściana graniastosłupa jest prostokątem, więc ściany boczne mają łącznie 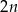 przekątnych. Do tego musimy dodać przekątne podstaw – na mocy wzoru na liczę przekątnych
przekątnych. Do tego musimy dodać przekątne podstaw – na mocy wzoru na liczę przekątnych  -kąta wypukłego, podstawy mają
-kąta wypukłego, podstawy mają
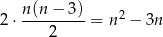
przekątnych, więc w sumie przekątnych jest
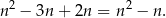
Rozwiązujemy równanie
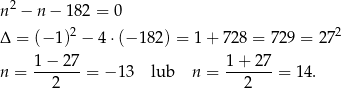
Odrzucamy rozwiązanie ujemne i otrzymujemy 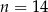 .
.
Odpowiedź: B

