Zadanie nr 1515118
Dla jakiej wartości parametru 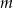 punkt przecięcia prostych
punkt przecięcia prostych 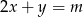 i
i 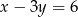 należy do osi
należy do osi 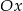 ?
?
A) dla 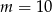 B) dla
B) dla 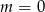 C) dla
C) dla 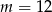 D) dla
D) dla 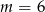
Rozwiązanie
Sposób I
Wyznaczmy punkt przecięcia prostej 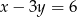 z osią
z osią 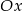 .
.

W tym samym punkcie pierwsza prosta ma przecinać 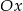 , więc musi być
, więc musi być

Sposób II
Wyznaczmy punkt wspólny danych prostych
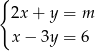
Odejmujemy od pierwszego równania drugie pomnożone przez 2 (żeby skrócić  ) i mamy
) i mamy
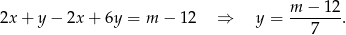
Jeżeli punkt wspólny ma leżeć na osi 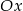 , to musi być
, to musi być 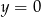 , czyli
, czyli 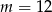 .
.
Odpowiedź: C

