Zadanie nr 1515308
W trójkącie prostokątnym o polu 15 najkrótszy bok ma długość 3. Obwód tego trójkąta jest równy
A) 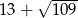 B)
B) 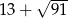 C)
C) 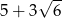 D)
D) 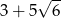
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
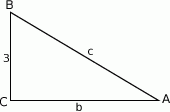
Z podanego pola obliczamy długość drugiej przyprostokątnej
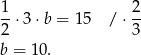
Korzystając z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej.
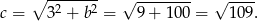
Obwód trójkąta jest więc równy
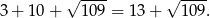
Odpowiedź: A

