Zadanie nr 1576909
Punkty 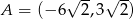 i
i 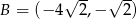 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 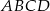 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 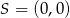 . Środek boku
. Środek boku 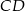 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 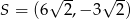 B)
B) 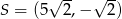 C)
C) 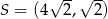 D)
D) 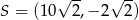
Rozwiązanie
Szkicujemy równoległobok.
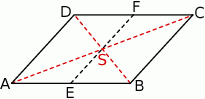
Sposób I
Jeżeli początek układu jest środkiem symetrii równoległoboku, to łatwo wyznaczyć (odgadnąć) współrzędne pozostałych wierzchołków równoległoboku.
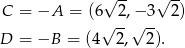
W takim razie środek 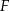 odcinka
odcinka 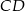 ma współrzędne
ma współrzędne
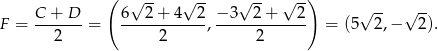
Sposób II
Skoro początek układu jest środkiem symetrii równoległoboku, to jest on środkiem odcinka 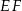 , gdzie
, gdzie 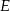 i
i 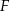 to odpowiednio środki odcinków
to odpowiednio środki odcinków 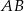 i
i 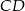 . Mamy zatem
. Mamy zatem
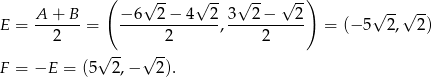
Odpowiedź: B

