Zadanie nr 1751143
Punkty 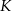 i
i 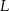 są środkami przyprostokątnych
są środkami przyprostokątnych 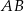 i
i 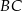 trójkąta prostokątnego
trójkąta prostokątnego 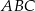 . Punkty
. Punkty 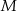 i
i 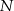 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 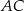 tak, że odcinki
tak, że odcinki 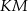 i
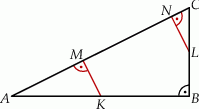
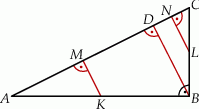
i 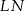 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 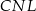 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 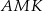 jest równe 5.
jest równe 5.
Zatem pole trójkąta 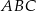 jest równe
jest równe
A) 32 B) 16 C) 28 D) 18
Rozwiązanie
Dorysujmy wysokość 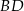 trójkąta
trójkąta 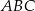 .
.
Zauważmy teraz, że trójkąt 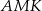 jest podobny do trójkąta
jest podobny do trójkąta 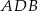 w skali
w skali 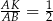 . podobnie trójkąt
. podobnie trójkąt 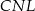 jest podobny do trójkąta
jest podobny do trójkąta 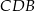 w skali
w skali 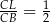 . Mamy stąd
. Mamy stąd
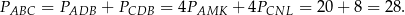
Odpowiedź: C

