Zadanie nr 1811645
Liczba przekątnych wielokąta wypukłego jest 6 razy większa od liczby jego boków. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 15 B) 14 C) 13 D) 12
Rozwiązanie
Oznaczmy przez  szukaną liczbę boków. Ze wzoru na liczę przekątnych
szukaną liczbę boków. Ze wzoru na liczę przekątnych  -kąta wypukłego otrzymujemy równanie
-kąta wypukłego otrzymujemy równanie
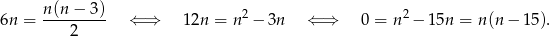
Ponieważ wielokąt musi mieć przynajmniej 3 boki, więc rozwiązaniem jest 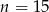 .
.
Odpowiedź: A

