Zadanie nr 2016588
Prosta 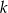 ma równanie
ma równanie 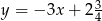 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 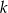 , przechodzącej przez punkt
, przechodzącej przez punkt 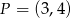 .
.
A) 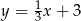 B)
B) 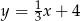 C)
C) 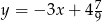 D)
D) 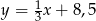
Rozwiązanie
Sposób I
Oznaczmy szukaną prostą przez 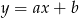 . Proste mają być prostopadłe, więc iloczyn ich współczynników kierunkowych musi być równy -1.
. Proste mają być prostopadłe, więc iloczyn ich współczynników kierunkowych musi być równy -1.
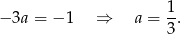
Podstawiamy punkt 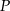 do równania i wyznaczamy wyraz wolny
do równania i wyznaczamy wyraz wolny
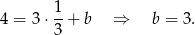
Zatem szukana prosta ma równanie
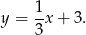
Sposób II
Szukana prosta musi być prostopadła do danej, więc musi mieć współczynnik kierunkowy 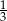 , co eliminuje jedną odpowiedź. W pozostałych podstawiamy
, co eliminuje jedną odpowiedź. W pozostałych podstawiamy 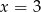 i sprawdzamy, czy wychodzi 4.
i sprawdzamy, czy wychodzi 4.
Odpowiedź: A

