Zadanie nr 2132459
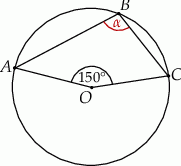
Punkt 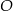 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 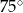 B)
B) 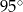 C)
C) 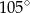 D)
D) 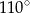
Rozwiązanie
Sposób I
Na mocy twierdzenia o kątach wpisanym i środkowym opartych na tym samym łuku, kąt wklęsły 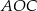 ma miarę
ma miarę 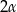 .
.
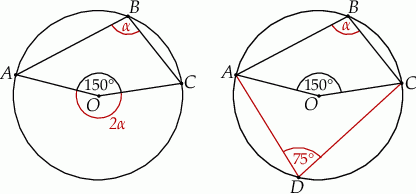
Zatem
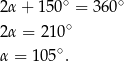
Sposób II
Wybierzmy punkt 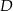 na łuku
na łuku 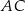 tak jak na prawym obrazku. Wtedy
tak jak na prawym obrazku. Wtedy 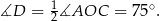 Ponieważ w czworokącie wpisanym w okrąg sumy przeciwległych kątów są równe
Ponieważ w czworokącie wpisanym w okrąg sumy przeciwległych kątów są równe  , więc
, więc
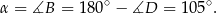
Odpowiedź: C

