Zadanie nr 2524252
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 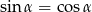 . Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
A) 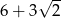 B)
B) 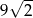 C)
C) 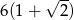 D)
D) 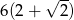
Rozwiązanie
Zaczynamy od rysunku
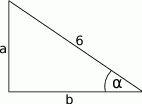
Najpierw zastanówmy się nad równości sinusa i cosinusa
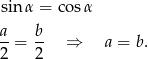
Z twierdzenia Pitagorasa wyznaczamy długości boków
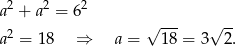
Zatem obwód jest równy
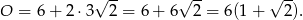
Odpowiedź: C

