Zadanie nr 2642222
Dane są dwa prostopadłościany podobne: 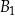 oraz
oraz 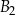 . Objętość prostopadłościanu
. Objętość prostopadłościanu 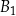 jest równa
jest równa 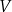 , a objętość prostopadłościanu
, a objętość prostopadłościanu 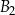 jest równa
jest równa 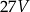 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 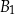 jest równe
jest równe 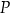 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 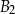 jest równe
jest równe
A) 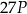 , , | B) 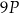 , , | C) 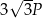 |
ponieważ stosunek pól powierzchni całkowitych prostopadłościanów podobnych jest równy
| 1) | stosunkowi objętości tych prostopadłościanów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku objętości tych prostopadłościanów. |
| 3) | kwadratowi stosunku długości odcinków odpowiadających w obu prostopadłościanach. |
Rozwiązanie
Jeżeli 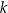 jest skalą podobieństwa prostopadłościanu
jest skalą podobieństwa prostopadłościanu 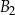 do prostopadłościanu
do prostopadłościanu 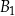 , to
, to
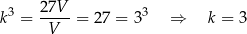
(bo objętość zmienia się jak sześcian skali podobieństwa). Wtedy stosunek pól powierzchni tych prostopadłościanów jest równy

(pole zmienia się jak kwadrat skali podobieństwa). Pole powierzchni prostopadłościanu 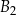 jest więc równe
jest więc równe 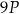 .
.
Odpowiedź: B, 3

