Zadanie nr 2762417
W układzie współrzędnych na płaszczyźnie dany jest odcinek 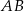 o końcach w punktach
o końcach w punktach 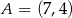 ,
, 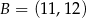 . Punkt
. Punkt 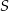 leży wewnątrz odcinka
leży wewnątrz odcinka 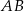 oraz
oraz 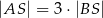 . Wówczas
. Wówczas
A) 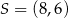 B)
B) 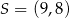 C)
C) 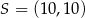 D)
D) 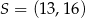
Rozwiązanie
Sposób I
Szkicujemy opisaną sytuację.
Jeżeli 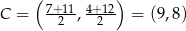 jest środkiem odcinka
jest środkiem odcinka 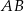 , to
, to  jest środkiem odcinka
jest środkiem odcinka  . Zatem
. Zatem
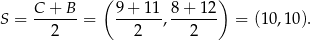
Sposób II
Tym razem użyjemy rachunku wektorowego. Jeżeli 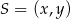 , to
, to
![−→ −→ AS = 3SB [x − 7,y − 4] = 3[11 − x ,1 2− y] = [3 3− 3x ,36 − 3y].](https://img.zadania.info/zad/2762417/HzadR7x.gif)
Mamy stąd
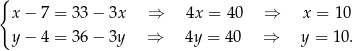
Zatem 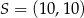 .
.
Odpowiedź: C

