Zadanie nr 2973012
Dany jest prostokąt 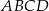 o wierzchołkach
o wierzchołkach 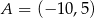 ,
, 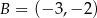 ,
, 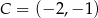 i
i 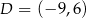 . Który z podanych punktów leży na okręgu opisanym na prostokącie
. Który z podanych punktów leży na okręgu opisanym na prostokącie 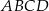 ?
?
A) 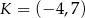 B)
B) 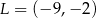 C)
C) 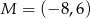 D)
D) 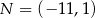
Rozwiązanie
Szkicujemy opisaną sytuację.
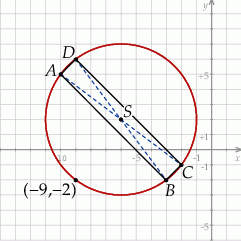
Środkiem okręgu opisanego na prostokącie 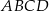 jest punkt przecięcia się jego przekątnych, czyli punkt
jest punkt przecięcia się jego przekątnych, czyli punkt
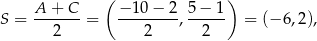
a jego promień ma długość
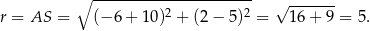
Wystarczy teraz sprawdzić, dla którego z podanych punktów odległość od 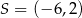 jest równa 5. Sprawdzamy kolejno
jest równa 5. Sprawdzamy kolejno
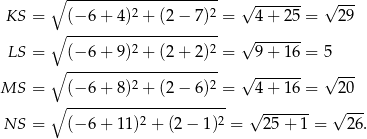
Odpowiedź: B

