Zadanie nr 2988252
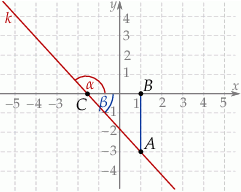
Na rysunku przedstawiona jest prosta 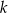 , przechodząca przez punkt
, przechodząca przez punkt 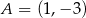 oraz przecinająca oś
oraz przecinająca oś 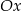 w punkcie
w punkcie 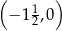 .
.
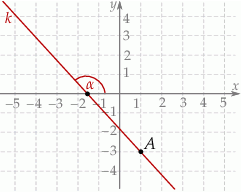
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
A) 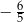 B)
B) 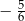 C)
C) 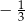 D)
D) 
Rozwiązanie
Sposób I
Napiszmy równanie prostej przedstawionej na rysunku.
Szukamy równania postaci 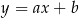 i podstawiamy współrzędne podanych punktów
i podstawiamy współrzędne podanych punktów 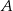 i
i 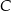 .
.
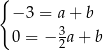
Odejmujemy od pierwszego równania drugie (żeby skrócić 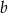 ) i mamy
) i mamy
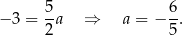
Ponieważ interesujący nas tangens to dokładnie współczynnik kierunkowy  prostej
prostej 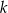 mamy
mamy
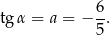
Sposób II
Tym razem patrzymy na trójkąt prostokątny 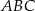 .
.
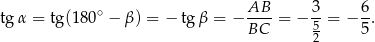
Odpowiedź: A

