Zadanie nr 3015725
Promień okręgu, przechodzącego przez cztery wierzchołki prostokąta, ma długość 2, a kąt ostry między przekątnymi tego prostokąta ma miarę 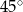 . Niech
. Niech 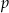 oznacza pole prostokąta. Wtedy
oznacza pole prostokąta. Wtedy
A) 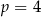 B)
B) 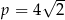 C)
C) 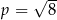 D)
D) 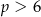
Rozwiązanie
Zaczynamy od rysunku
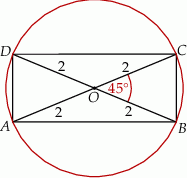
Sposób I
Korzystamy ze wzoru na pole czworokąta z przekątnymi.
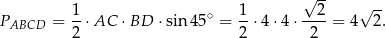
Sposób II
Przekątne dzielą prostokąt na 4 trójkąty o równych polach, zatem pole prostokąta możemy obliczyć korzystając ze wzoru na pole trójkąta z sinusem.
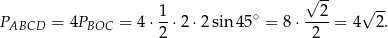
Odpowiedź: B

