Zadanie nr 3112808
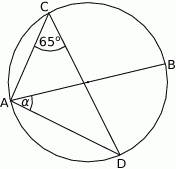
Na rysunku odcinek 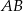 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 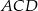 ma miarę
ma miarę 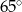 . Miara kąta
. Miara kąta 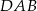 jest równa
jest równa
A) 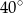 B)
B) 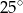 C)
C) 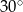 D)
D) 
Rozwiązanie
Sposób I
Patrzymy na trójkąt 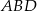 .
.
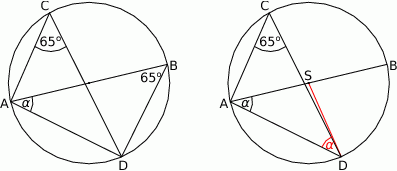
Ponieważ 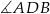 jest oparty na średnicy, więc
jest oparty na średnicy, więc
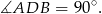
Ponadto, kąty 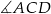 i
i 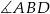 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc
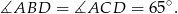
Zatem
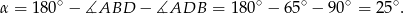
Sposób II
Niech 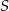 będzie środkiem okręgu i dorysujmy promień
będzie środkiem okręgu i dorysujmy promień 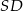 . Wtedy
. Wtedy
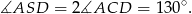
Trójkąt 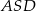 jest równoramienny, więc
jest równoramienny, więc
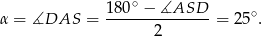
Odpowiedź: B

