Zadanie nr 3184598
Okrąg o równaniu 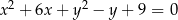 przekształcono w jednokładności o środku
przekształcono w jednokładności o środku 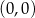 i skali
i skali 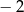 . Otrzymany okrąg ma równanie
. Otrzymany okrąg ma równanie
A) 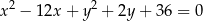 B)
B) 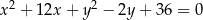
C) 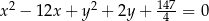 D)
D) 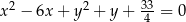
Rozwiązanie
Przekształćmy dane równanie okręgu tak, aby było widać jaki jest jego środek i promień
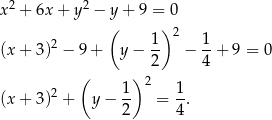
Jest to więc okrąg o środku 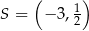 i promieniu
i promieniu 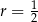 . Szkicujemy tę sytuację.
. Szkicujemy tę sytuację.
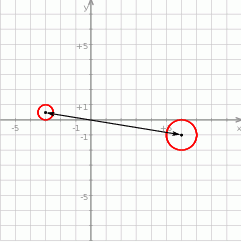
Z obrazka powinno być jasne, że po wykonaniu jednokładności opisanej w treści zadania, otrzymamy okrąg o środku 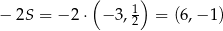 i promieniu
i promieniu 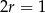 . Jest to więc okrąg o równaniu
. Jest to więc okrąg o równaniu
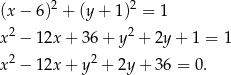
Odpowiedź: A

