Zadanie nr 4625781
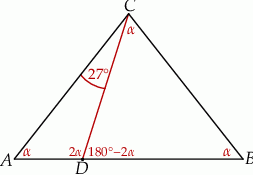
W trójkącie 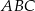 , w którym
, w którym 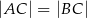 , na boku
, na boku 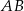 wybrano punkt
wybrano punkt 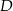 taki, że
taki, że 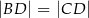 oraz
oraz 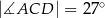 (zobacz rysunek).
(zobacz rysunek).
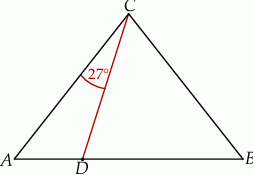
Wynika stąd, że kąt 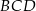 ma miarę
ma miarę
A) 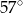 B)
B) 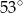 C)
C) 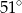 D)
D) 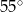
Rozwiązanie
Oznaczmy 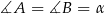 .
.
Trójkąt 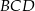 jest równoramienny, więc
jest równoramienny, więc 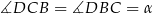 i
i
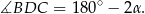
Stąd 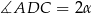 i w trójkącie
i w trójkącie 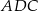 mamy
mamy
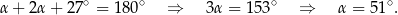
Odpowiedź: C

