Zadanie nr 4719632
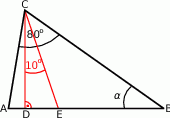
Dany jest trójkąt 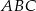 o kącie
o kącie 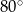 przy wierzchołku
przy wierzchołku 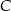 . Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka
. Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka 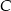 ma miarę
ma miarę 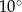 . Wynika stąd, że kąt
. Wynika stąd, że kąt  jest równy
jest równy
A) 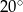 B)
B) 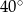 C)
C) 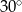 D)
D) 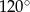
Rozwiązanie
Zaczynamy od rysunku
Sposób I
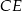 jest dwusieczną kąta
jest dwusieczną kąta 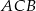 , więc
, więc
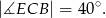
Stąd
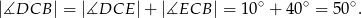
Teraz już łatwo obliczyć szukany kąt
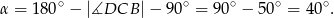
Sposób II
Liczymy
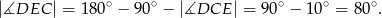
Stąd
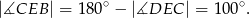
Teraz już łatwo obliczyć szukany kąt
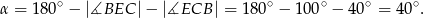
Odpowiedź: B

