Zadanie nr 4756282
Okrąg o równaniu 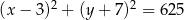 jest styczny do okręgu o środku
jest styczny do okręgu o środku 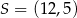 i promieniu
i promieniu  . Wynika stąd, że
. Wynika stąd, że
A) 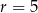 B)
B) 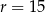 C)
C) 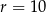 D)
D) 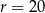
Rozwiązanie
Przypomnijmy, że jeżeli okrąg jest dany równaniem
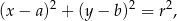
to 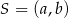 jest środkiem tego okręgu, a
jest środkiem tego okręgu, a  jego promieniem. W takim razie pierwszy z podanych okręgów ma środek
jego promieniem. W takim razie pierwszy z podanych okręgów ma środek 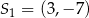 i promień
i promień 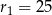 .
.
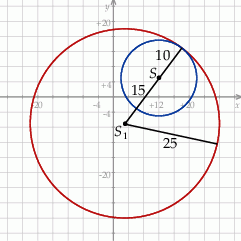
Jest to dość duży okrąg – gdy go naszkicujemy robi się jasne, że podany punkt 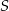 znajduje się w jego wnętrzu. W takim razie okręgi te muszą być styczne wewnętrznie i mamy
znajduje się w jego wnętrzu. W takim razie okręgi te muszą być styczne wewnętrznie i mamy
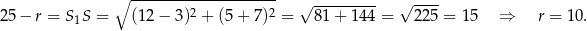
Odpowiedź: C

